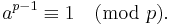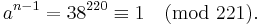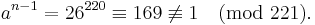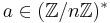Fermat primality test

The Fermat primality test is a probabilistic test to determine if a number is probable prime.

1 Concept
2 Example
3 Algorithm and running time
4 Flaw
5 Applications
6 References

Concept

Fermat's little theorem states that if p is prime and 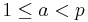$1 \le a < p$ , then

$a^{p-1} \equiv 1 \pmod{p}.$

If we want to test if p is prime, then we can pick random a's in the interval and see if the equality holds. If the equality does not hold for a value of a, then p is composite. If the equality does hold for many values of a, then we can say that p is probable prime.

It might be in our tests that we do not pick any value for a such that the equality fails. Any a such that

$a^{n-1} \equiv 1 \pmod{n}$

when n is composite is known as a Fermat liar. Vice versa, in this case n is called Fermat pseudoprime to base a.

If we do pick an a such that

$a^{n-1} \not\equiv 1 \pmod{n}$

then a is known as a Fermat witness for the compositeness of n.

Example

Suppose we wish to determine if n = 221 is prime. Randomly pick 1 ≤ a < 221, say a = 38. Check the above equality:

$a^{n-1} = 38^{220} \equiv 1 \pmod{221}.$

Either 221 is prime, or 38 is a Fermat liar, so we take another a, say 26:

$a^{n-1} = 26^{220} \equiv 169 \not\equiv 1 \pmod{221}.$

So 221 is composite and 38 was indeed a Fermat liar.

Algorithm and running time

The algorithm can be written as follows:

Inputs: n: a value to test for primality; k: a parameter that determines the number of times to test for primality
Output: composite if n is composite, otherwise probably prime
repeat k times:
   pick a randomly in the range [1, n − 1]
   if , then return composite
return probably prime

Using fast algorithms for modular exponentiation, the running time of this algorithm is O(k × log²n × log log n × log log log n), where k is the number of times we test a random a, and n is the value we want to test for primality.

Flaw

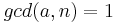There are infinitely many values of $n$ (known as Carmichael numbers) for which all values of $a$ for which $gcd(a, n) = 1$ are Fermat liars. While Carmichael numbers are substantially rarer than prime numbers,^[1] there are enough of them that Fermat's primality test is often not used in favor of other primality tests such as Miller-Rabin and Solovay-Strassen.

In general, if $n$ is not a Carmichael number then at least half of all

$a\in(\mathbb{Z}/n\mathbb{Z})^*$

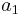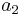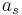are Fermat witnesses. For proof of this, let $a$ be a Fermat witness and $a_1$ , $a_2$ , ..., $a_s$ be Fermat liars. Then

$(a\cdot a_i)^{n-1} \equiv a^{n-1}\cdot a_i^{n-1} \equiv a^{n-1} \not\equiv 1\pmod{n}$

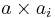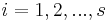and so all $a \times a_i$ for $i = 1, 2, ..., s$ are Fermat witnesses.

Applications

The encryption program PGP uses this primality test in its algorithms. The chance of PGP generating a Carmichael number is less than 1 in 10⁵⁰, which is more than adequate for practical purposes.

References

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein (2001). "Section 31.8: Primality testing". Introduction to Algorithms (Second Edition ed.). MIT Press; McGraw-Hill. p. 889–890. ISBN 0-262-03293-7.

^ Erdös' upper bound for the number of Carmichael numbers is lower than the prime number function n/log(n)

Number-theoretic algorithms

Primality tests	AKS · APR · Baillie–PSW · ECPP · Elliptic curve · Pocklington · Fermat · Lucas · Lucas–Lehmer · Lucas–Lehmer–Riesel · Proth's theorem · Pépin's · Solovay–Strassen · Miller–Rabin · Trial division

Sieving algorithms	Sieve of Atkin · Sieve of Eratosthenes · Sieve of Sundaram · Wheel factorization

Integer factorization algorithms	CFRAC · Dixon's · ECM · Euler's · Pollard's rho · p − 1 · p + 1 · QS · GNFS · SNFS · rational sieve · Fermat's · Shanks' square forms · Trial division · Shor's

Multiplication algorithms	Ancient Egyptian multiplication · Karatsuba algorithm · Toom–Cook multiplication · Schönhage–Strassen algorithm · Fürer's algorithm

Discrete logarithm algorithms	Baby-step giant-step · Pollard rho · Pollard kangaroo · Pohlig–Hellman · Index calculus · Function field sieve

GCD algorithms	Binary GCD · Euclidean · Extended Euclidean · Lehmer's

Modular square root algorithms	Cipolla · Pocklington's · Tonelli–Shanks

Other algorithms	Chakravala · Cornacchia · integer relation algorithm · integer square root · Modular exponentiation · Schoof's

Italics indicate that algorithm is for numbers of special forms; bold indicates deterministic algorithm for primality tests (current article is always in bold).